History of Abacus and Ancient Computing
December 2019. Vladimir Esaulov
It may be hard to imagine today that long ago people used to count using scratches (tally marks) on sticks or counted with the help of small stones or just with fingers. The word calculate comes from the Latin calculus, which means small stone. In the following we look at various ancient counting aides and devices. Additional examples of some of these may be seen in the collection. This page covers :
- Tally sticks: bones or wood pieces with notches. The word tally comes from Latin talea – twig or cutting.
- Tokens: variously shaped clay counters as an alternative to cruder pebbles.
- Counting boards, including coin counting boards (Palaka, Zeni Masu). The Salamis tablet, medieval counting boards, the Exchequer and Incan Yupana.
- The Abacus (Roman, chinese-suanpan, japanese-soroban, mexican-nepohualtzintzin)
- Bead counters on strings used as prayer counters, podometers etc.
- Various unusual abaci possibly made to order for specific use.
Some related artworks are shown along the text and at the end of the section. In China the Abacus is a symbol of prosperity and advancement in economic and academic areas. This has also led to appearance of abacus jewellery and display items.
TALLY STICKS OR PALEOLITHIC COUNTING AIDS.
Tally sticks, made of wood or bone, have been used since ancient times as a “data recording” device or memory aid to record numbers, quantities, or even messages. Tally sticks first appeared as animal bones carved with notches during the Upper Paleolithic. Use of tally sticks has been mentioned by Pliny the Elder (AD 23–79) in his Naturalis Historia ca 77. Marco Polo (1254–1324) referred to the use of the tally in Chin (ref.1). Tally sticks as a recording device are in some way similar to records using knotted strings described elsewhere in these pages. A variant of this approach, consisted in the use of a split tally stick to provide a copy of a common transaction to two parties as a receipt. In this case a piece of wood was marked with notches perpendicular to its length and then split lengthwise so each party to the transaction received one half of the marked stick as proof and the two parts could be unambiguously matched together. The half tally stick came to be acceptable as money and could be passed on to other parties.
The Case of the Paleolithic Counting devices. Archelogical excavations have come up with several artefacts, which have become famous because of interpretations of their uses as mathematical tools. or just using fingers
In 1937, an 18 cm-long radial wolf bone was discovered at Věstonice in the Czech Republic and dated to 30,000 years ago. Karel Absolon presented it in The Illustrated London News (1937), pointing out that it had fifty-five notches incised on it. First came 25 in groups of five, then a notch of double length, followed by a similar double notch that began a series of 30. This would prove the mammoth hunters ability to count. It was thought that the groups of five were suggested by the five fingers of a hand.
The most famous of such artefacts is possibly the Ishango bone (ref.2). Excavations conducted in 1950 in Ishango in the north-east of the Democratic Republic of Congo by the Belgian geologist-archelogist Jean de Heinzelin unearthed an object made up of a small piece of quartz fixed on top of an animal bone handle (D.R. Congo, ex Zaire). It has a series of notches in three columns which can be seen in the image below. The so called Ishango bone has been dated to the Upper Paleolithic Period around 22000 years ago. It is on permanent exhibition at the Royal Belgian Institute of Natural Sciences, Brussels, Belgium (ref.2). A second similar object was found by de Heinzelin in 1959. The 14-cm long bone has 90 notches on six sides.
Various theories have been proposed to explain the reasons behind the existence of the notches on the Ishango bone ranging from creating a better grip on the handle, as a memory aid, to more sophisticated mathematical uses (ref.3-7). The latter daring ideas stem from a degree of organization of the notches, which led de Heinzelin to suggest they are a type of mathematical reckoning device. Some have evoked a relation to prime numbers. They have also been thought to have a relation to lunar cycles as suggested by Alexander Marshack. The prime number relationionship has been contested by Peter Rudman (ref 6.) and others. The currently prevalent interpretation, due to Vladimir Pletser and Dirk Huylebrouck (ref 3,5) is that, in the words of the authors:
“1.) The Ishango bone, dated from 22,000 years, can be considered as the oldest mathematical tool of humankind because the arrangement of the notches on three columns suggests an arithmetical intention. …2) In addition, it appears that several bases are used in this elementary arithmetic: the base 10 and base 12 with its submultiples 3, 4 and 6. The geometric arrangement of the notches in the various groupings on the three columns allows to compute other basic arithmetic operations”.
This has been criticized by Olivier Keller (ref.4 and see rebuttal in ref.5). Yet another such artefact is the Lebombo bone, a 35,000-year-old baboon fibula bearing 29 notches, was discovered in a cave in the Lebombo mountains in Swaziland. Some claim it to be “Oldest Mathematical Artefact” (ref.7).
COUNTING WITH PEBBLES AND BEYOND. TOKENS, THE COUNTING BOARD AND THE ABACUS.
At some point the idea to use loose objects like pebbles to count appeared. Counting directly with stones would be cumbersome: if you have to count up to 10000: you need ten thousand pebbles…. A solution could be to use stones of different sizes to represent different numbers: small stone =1, bigger stone=10, still bigger stone = 100 etc.
TOKENS.
Long ago dating back to 7500 BC there appeared different types of “tokens“- clay counters of different sizes and shapes, which are thought to have been used to count and communicate. These have been found in an extensive region stretching from the Mediterranean to Pakistan and extensively studied by Denise Schmandt-Besserat and others. The shapes are thought to have been representative of a specific type of object and also to given quantities. Thus concerning tokens found in Tepe Zagheh, located in the Qazvin Plain of Central Plateau of Iran Denise Schmandt-Besserat and Niloufar Moghimi write (ref. 8) (figures and references in their text are edited out):
“As decoded by the earliest written tablets of 3100 BCE, each token shape was the symbol for a particular commodity. Isosceles cones, spheres and disks stood for various measures of cereals. A small cone and a small sphere were respectively equivalent to one peck and one bushel of cereals. A large cone, a large sphere and a flat disk stood for larger measures, perhaps corresponding to one bag (3 bushels), one cauldron (36 bushels) or one load (40 bushels). Ovoids represented jars of oil; each lenticular disk stood for «a flock» of domesticated small cattle, while tetrahedrons were units of work….“.
This initial counting method is called concrete as it refers to a specific object and is not abstract counting with numbers representing any object as we do today. This approach appeared later.
During commercial transactions, in order to avoid fraud and ensure that the number and type of tokens were not modified, they were sealed into a ball-shaped baked clay envelope. For further security the exterior of the ball was embossed with seals and signs representing the type of token that the ball contained. Early tokens had simple shapes, which with time became very varied, had engraved markings and were also carried on strings. Tokens gave way to cuneiform writing (around 3000 BC), but were not completely abandoned and the two were used together.

COUNTING BOARDS.
The counting board was invented when someone thought of placing pebbles or other objects on lines marked on a flat surface, and assigning an increasing order of magnitude to the objects on subsequent lines. The Latin word abacus comes from Greek άβακασ – board or table. Possibly its origin is semitic and comes from the word abq meaning sand, which suggests using a sand board to count. The sand abacus was used in the Persian world. Islamic astrologers used dust (sand) covered tablets (takht) on which they could make and erase calculations (ref 9, 10). The oldest written information about the abacus, appears to be from the Greek historian Herodotus (480-425 B.C.), who mentioned also, that the ancient Egyptians used the abacus.
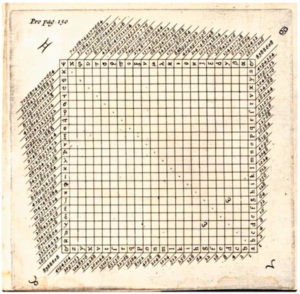
The oldest surviving counting board is the Salamis Board or Tablet (c. 300 BC), a white marble board, that was discovered on the Greek island of Salamis in 1846. It is now in the Greek National Museum of Epigraphy in Athens. The Salamis board is about 150 x 75 x 4.5 cm. It is engraved with Greek letters and a set of lines (see image). There are three sets of Greek symbols on the left, right and bottom of the board, which are numbers from the acrophonic system. A set of parallel lines are engraved into the board. There is a series of five parallel lines and, below them, another eleven parallel lines. These are divided in half by a perpendicular line. The perpendicular line is marked with a semicircle at the intersection with the top horizontal line and the intersections with the third, sixth and ninth of these lines are marked with a cross.
It is thought that counting was performed by placing pebbles on the horizontal lines or between them. The lines from bottom to top corresponded to powers of ten: a pebble placed on the bottom line represented one, on the next one 10 and the following one 100. A pebble between the lines represented half the value of a pebble on the line above it. So a pebble between the first and second line represented 5 and between the second and third line represented 50. The vertical line separated positive and negative portions of the board: pebbles on the right side of the vertical line represent positive digits and those on the left side of the line represent negative digits.
An ancient depiction of a man possibly using a counting board appears on the so called Darius vase (circa 340-320BC) decorated by the Apulian vase painter Darius, which was discovered in 1851 near Canosa di Puglia and is located at the Museo Archaeologico Nazionale.

Counting Boards in Europe. The use of counting boards in Europe continued till around the 16th century, when they were superseded by written counting methods. There do not seem to be any surviving counting boards except for one in a Strasbourg museum which dates back to the 16th century. Several 16th century texts describe the use of the counting board and address the use of the Hindu-Arabic numerals. Images of cover and some other pages of some of these texts are shown here.

The 1503 encyclopedia text of Margarita philosophica (Pearl of Wisdom) of Gregor Reisch (1467 – 1525), which was used as a university textbook in the early sixteenth century, deals amongst other with the seven liberal arts composed of the basic trio called trivium of logic, rhetoric, grammar and followed by the quadrivium of arithmetic, music, geometry, and astronomy. It contains various engravings amongst which the famous engraving of Arithmetica (or the Allegory of Arithmetic) supervising a contest between Boethius, representing written calculation using Hindu-Arabic numbers, and Pythagoras, represented as using a counting board. Arithmetica can be seen looking towards Boethius with a benign smile.
The 16th century famous German mathematician Adam Ries, wrote several mathematical texts including Rechnung auff der linihen (1518) which contain explanation on the use of counting boards, with later texts Rechnung auff der linihen und federn… (1522) explaining also calculations with Hindu-Arabic numerals. The text was extremely popular and the book was republished many times.
The Exchequer: the British Counting Board. A Court of the Exchequer was set up in England in the 12th century during the reign of Henry I. Its original purpose was to audit money paid to the Crown. It later took on other functions, such as the collection of taxes, and acted as a court of law to decide what was legally owed to the Crown. A counting board, resembling a big chess board, was used to do the accounting. A treasurer, Richard Fitz Nigel, wrote ‘The Dialogue of the Exchequer’ in about 1179, which described its functioning.
The image (facsimile of Irish Manuscripts, volume III, plate xxxvii. ) shows the Exchequer of Ireland at work in the 15th century. It comes from a collection of documents known as the Red Book of the Exchequer, dating from the 13th – 16th centuries.
Here are some excerpts from his text as taken from the Yale University (italics were added):
I. What the Exchequer is, and what is the reason of this name.
Disciple. What is the exchequer?
Master. The exchequer is a quadrangular surface about ten feet in length, five in breadth, placed before those who sit around it in the manner of a table, and all around it it has an edge about the height of one’s four fingers, lest any thing placed upon it should fall off. There is placed over the top of the exchequer, moreover, a cloth bought at the Easter term, not an ordinary one but a black one marked with stripes, the stripes being distant from each other the space of a foot or the breadth of a hand. In the spaces moreover are counters placed according to their values; about these we shall speak below. Although, moreover, such a surface is called exchequer, nevertheless this name is so changed about that the court itself which sits when the exchequer does is called exchequer; so that if at any time through a decree any thing is established by common counsel, it is said to have been done at the exchequer of this or that year. As, moreover, one says today “at the exchequer,” so one formerly said ” at the tallies.”
D.What is the reason of this name ?
M. No truer one occurs to me at present than that it has a shape similar to that of a chess board.
D.Would the prudence of the ancients ever have called it so for its shape alone, when it might for a similar reason be called a table (tabularium) ?
M. I was right in calling thee painstaking. There is another, but a more hidden reason. For just as, in a game of chess, there are certain grades of combatants and they proceed or stand still by certain laws or limitations, some presiding and others advancing: so, in this, some preside, some assist by reason of their office, and no one is free to exceed the fixed laws; as will be manifest from what is to follow. Moreover, as in chess the battle is fought between kings, so in this it is chiefly between two that the conflict takes place and the war is waged, the treasurer, namely, and the sheriff who sits there to render account; the others sitting by as judges, to see and to judge. ………………………..
V. What is the office of the President, and of all those who sit there officially; and what the arrangement of the seats. ………………….
As to the Calculator.
This is his business: according to the usual course of the exchequer, not according to arithmetical laws. Thou wilt remember, I presume, my saying that on the exchequer was placed a cloth divided by stripes, in the spaces of which heaps of cash are placed. Now the calculator sits in the middle of the side, that he may be visible to all, and that his busy hand may have free course. He has placed already at his right hand, in the lower space, a heap of pennies from 11 down; in the second, of shillings from 19 down; but in the third, of pounds.And this heap, indeed, ought to be opposite and directly facing him, for in the ordinary accounts of the sheriff it is the medium; in the fourth is the heap of the twenties; in the fifth, of the hundreds; in the sixth, of the thousands; in the seventh, but rarely, of the ten thousands of pounds;rarely, I say, that is when, through the king or his mandate, the account for the receipts of the whole kingdom is received by the nobles of the kingdom from the treasurer and the chamberlains. Moreover, it is lawful for the calculator to put a silver piece in place of ten shillings, or a gold obol in place of ten pounds, so that the account may be more quickly made. He must take care, however, lest his too hasty hand proceed before his tongue, or the reverse; but at the same time that he counts he shall place the counter and designate the number, lest there be an error in the number. The sum, therefore, which is required from the sheriff being arranged in heaps, those sums which have been paid in, either to the treasury or otherwise, are arranged below, likewise in heaps. But if it be a farm by tale which is required of him, or any other debt which can be satisfied by tale only, there shall simply be made a deduction of the lower from the upper sum, and he shall be bounder for the rest; it shall be done otherwise, however if he be about to pay a blank farm; as will be more fully shown when we treat of the sheriff’s business.
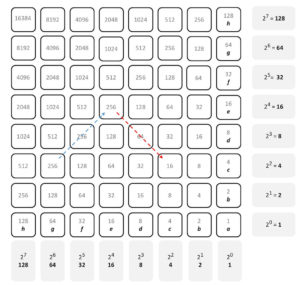
Napier’s Chessboard binary abacus. In the early 17th century John Napier of Merchiston (1550-1617), who is famous for the invention of logarithms, proposed a “binary” chessboard abacus, shown in the image here. Its functioning is described in the third part of his Rabdologiae dealing with his other two computational aids (the “bones” and “promptuary”; see elsewhere on these pages). This counting board could be used to perform the four arithmetical operations and calculate square roots using a binary “location” arithmetic, in which counters were moved around the board following simple rules. A reduced version of his abacus using a standard chess or cheker board, which was common in Napier’s time and could thus be easily adapted for this use, is shown along with the values of each square, which represents powers of 2. The bottom and right edges, are labelled using powers of 2 and Napier labelled each row and column with letters. Note that binary maths, as we use today, had not yet been invented, but multiplication and division by two was known from ancient times.
The squares on the board represent progressively increasing powers of two, when moving from left to right along a row or up a column. Any number could be expressed by placing counters at appropriate locations along a row, whence the notion of “location” arithmetic. Locations are denoted by letter combinations designating rows and columns. Thus 40 could be represented with counters placed in the first bottom “a” row one each at f-a(=32), d-a(=8)8, or else e-a (=16), d-a(=8), c-a(=4) b-a(=2) or alternatively placing two counters e.g. in the third row at e-a(2×16) and c-a(2×4). Similarly 40 can be represented by placing counters in the third “c” row at d-c(=32) and b-c (=8). Moving a counter left or right by one position would double or half its value. Moving diagonally from left to right conserved its value (blue arrow), whereas a diagonal motion from right to left represented a division by four (red arrow). We do not go into the operation of the abacus on this page, but the interested reader can refer to the paper by Kolpas and Tomash and some nice videos on the internet. The abacus, contrarily to Napier’s bones calculating aid, did not gain much popularity.
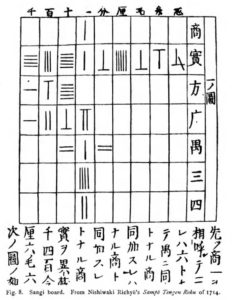
Asian Counting Boards. The Chinese started to use counting boards around the 4th century BC. The board was a plate, divided into columns, and calculations were made using sticks made of wood or bone, which were combined placing them vertically or horizontally to represent numbers (rod numerals) as shown in the image. Positive and negative numbers were distinguished by the colour or by the shape of the stick, e.g. red for positive and black for negative. In the Chinese counting board, the rightmost column denoted units, the next—tens, etc.They were placed on a counting board, like a checkerboard, giving a clear delineation of the place values. To avoid confusion, the orientation of the rods alternated between being placed vertically and horizontally from one place value to the next. There was no zero, but an empty place was left, which around 1200 was replaced by a circle symbol O.
Several Chinese mathematical texts give explanations on how to use the counting board. Sun Zi, in the first chapter of the Sunzi suanjing (Sun Zi’s Mathematical Manual), gives instructions on using counting rods to multiply, divide, and compute square roots. The Chinese mathematical text of the Han dynasty period (206 B.C. to A.D. 220) — Jiu zhang suan shu (Nine Chapters on the Mathematical Art; unknown author with later compilation and commentaries by e.g. Liu Hui, 3rd century AD), gives details of algebraic operations on the counting board. The counting board was mostly replaced by the abacus by the 13-16th century AD during the Ming dynasty period. From China the counting board was transmitted to Korea, Japan and Vietnam.
The Travancore (Kerala, South India) Coin Counting Board – Palaka. The Palaka was used to quickly count small coins. The princely state of Travancore (1858 – 1949) used its own currency: the Travancore Rupee. It was subdivided into 7 fanam, each of 4 chakram, each of 16 cash. From 1901, silver coins issued were in denominations of 2 chakram, 4 chakrams, 7 chakram (quarter rupee) and 14 chakram (half rupee). The chakrams were small, flat pellets with symbols and numerals of small, circa 5mm size. The Palaka was a board with small circular sockets, each of which could hold a chakram. Spreading the chakrams accross a board with a fixed number of sockets made it easier to count them. The ivory board shown in the image has 42 sockets (ref.12). Some Palakas had areas with different numbers of sockets to make accounting simpler.
Similar coin counting boards were used in Japan. They are called Zeni Masu.
Counting boards of this type are still in use today as a Montessory teaching aids.
The Yupana. The Yupana was a mesoamerican counting board, which is discussed on our Yupana page here. An image of a board sometimes considered to be a Yupana is shown below.
The ABACUS.
The counting board was modified at some point and the loose counters were replaced by ones sliding in grooves or along wires giving rise to the abacus known and still in use till recently around the globe. This type of abacus was found in ancient Rome, China and many other countries. Where was it invented ? Ancient Rome, China ? It is hard to say: possibly, as this sometimes happens, independently in different regions, since it may not have been practical to use loose counters on counting boards.
An image on this page shows a bas-relief adorning a Roman sarcophagus of the 1st / 2nd centuries, preserved in the Capitoline Museum of Rome, Italy, in which a young calculator (dispensator), performs an arithmetic operation in front of his master. The calculatores or numerarii were computation masters charged to teach by means of the abacus or the “accountants”, intendants (dispensatores), in the houses of the patricians. When slaves practiced the same trades they were called calculones. (source encyclopedia).
The Roman Abacus. An Ancient Pocket Calculator. Only three Roman abacus appear to have survived. They are small handheld units of two types. An ivory abacus was part of a collection of IBM, whose current location is unknown. A description of this of abacus type is given by Marco Velseri in his letters in 1593 and his text Opera Historica et Philologica, Sacra et Profana (pages 818-820) shown here, featuring a rendering of the abacus. Another type, that may be seen in the Museum in Rome (inv 65054) and Aosta Museum of Archelogy (see image) is described by Raffaele Garrucci (ref. 13 and image here). In these there is a single long last slot on the right instead of the three small slots. Reproductions of later origin, may be found in the Bibliotheque Nationale de Paris and British Museum.
The Rome museum type abacus is 11.5 x 7.2 cm. It has straight slots cut into it along which counters could slide. There are eight long and eight short slots. The left most, seven long slots have 4 beads or counters, whereas the upper ones only one. The lower second from right slot (marked O or Ө ) has five beads. In the Aosta abacus and the one described by Garruci there is one extra long slot on the right, whereas in the Velseri version this slot is subdivided into three. In both cases this (or these three) slots have markings S, inverted letter C and a 2 (or Z). In case of a single long slot it had 4 beads and if there were 3 short slots then they had one, one and two beads respectively from top to bottom.
The slots marked I, X, C etc., indicate units, tens, hundreds etc whereas the upper ones represent multiples of five (5, 50, 500 …) and correspond to a bi-quinary decimal counting system. The two rightmost slots were used to count fractions in mixed base systems. The long slot marked with O(Ө ) with five beads allowed for the counting of 1/12 of a whole unit called an uncia (from which the English words inch and ounce are derived). This is because many Roman measures and the currency were fractions of 12. There are various possibilities as to what fractions of 12 the extra rightmost slot(s) positions could have been. We do not go into this in this short text.
Chinese Abacus- Suan Pan. The Chinese suanpan (counting tray) or Zhusuan (bead counting) appears to be first described in a 190 AD (Eastern Han Dynasty) book by Xu Yue: Supplementary Notes on the Art of Figures. The Suan Pan is a rectangular board divided by a bar in two unequal parts following its length, with rods placed along the width. In the classic old version, there are two beads on each rod in the upper deck called “heaven” and five beads on each rod in the bottom deck called “earth”. The number of rods is variable ranging usually from 9 to 13. The earliest painting with an abacus on it, is the scroll “Along the River During the Qingming Festival” (Qingming Shanghe Tu) attributed to Song Dynasty artist Zhang Zeduan, which shows a 15 rod abacus on the desk of a herbal medicine shop of Officer Zhao.
The beads are usually rounded and made of some hard wood. Counting, like in the Roman abacus is performed by moving them up or down towards the central bar. The zero position corresponds to the beads in both decks moved away from the central bar. The 5+2 bead configuration allows both decimal and hexadecimal computation. Suanpan techniques have been developed to do multiplication, division, addition, subtraction, square root and cube root operations. Other forms of the suanpan have six movable beads in each ordinate column (5+1) or in another more modern form these are reduced to five beads (4+1). Some modern suanpans have a “reset” button which pushes all the beads simultaneously to their zero positions.
The Japanese Soroban and Korean Chupan. The Abacus is supposed to have arrived in Japan around the 14th century, possibly via Korea. The Soroban started with the 5+2 bead configuration, which later changed to the 5+1 and then the most recent 4+1 bead systems, which apeared in the early 20th century. Different variants may still be found. Most of the Japanese sorobans have “double-cone” (or diamond) shaped beads, as oposed to the rounded chinese suanpan beads. Like the suanpan, sorobans normally have an odd number of rods. It is quite common to have very long sorobans with frequently up to 27 rods. In practive two sorobans can be placed lengthwise side by side. You can find detailed directions on the use of the Soroban in the book of Takashi Kojima (ref 19). The Korean Chupan has no special characteristics and usually resembles the Soroban. Some unusual sorobans are illustrated later in this section.
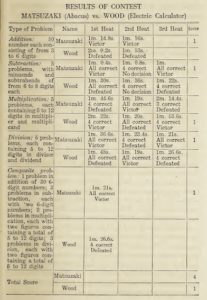
1946: the Abacus wins versus an electric calculator (almost). A now famous contest between the Japanese abacus and an electric calculating machine was held in Tokyo on November 12, 1946. The following is based on the text of Kojima (1954; see ref.19). The American representative of the calculating machine was Pvt. Thomas Nathan Wood of the 240th Finance Disbursing Section of General MacArthur’s headquarters, who had been selected as the most expert operator of the electric calculator in Japan. The Japanese representative was Mr. Kiyoshi Matsuzaki, a champion operator of the abacus in the Savings Bureau of the Ministry of Postal Administration.In reporting the contest, the organiser, the US Army newspaper Stars and Stripes wrote : “The machine age took a step backward yesterday at the Ernie Pyle Theater as the abacus, centuries old, dealt defeat to the most up-to-date electric machine now being used by the United States Government . . . The abacus victory was decisive.” The Nippon Times reported the contest as follows : ” Civilization, on the threshold of the atomic age, tottered Monday afternoon as the 2,000-year-old abacus beat the electric calculating machine in adding, subtracting, dividing and a problem including all three with multiplication thrown in, according to UP. Only in multiplication alone did the machine triumph…”. At the time the calculator was probably a desktop electro-mechanical one as desktop electronic calculators had not yet appeared.
Vietnamese Abacus: Bàn Tính or Bàn Tuần. Generally the Vietnamese abacus follows the Chinese-Japenese ones. One curious exception: a 5+5 bead abacus made of bone in a private collection, has two 13-rod decks with five beads each in the two decks. It is shown in the figure above.
The Russian Stcheti (счёты). The Russian Stcheti are usually quite large in size. The rectangular board has a single deck, with series of steel wires with groups of ten beads that are moved from right to left when counting. The wires usually bulge upward in the center. The beads are generally whitish or light brown in colour except for the two central beads that are black. This makes it easier to distinguish groups of five. Frequently in the lower part of the frame there are one or sometimes two rods with four beads only. These are related to the use of 1⁄4 value of Rubels, or 25 kopeks. The ten bead sections below these, count smaller decimal fractions (1/10, 1/100,..). This type of abacus is also common in middle eastern countries.
The Mesoamerican Abacus: the Nepohualtzintzin.
In the 1970s there appeared a theory that there had existed a Mesoamerican abacus with beads, for which the word “Nepohualtzintzin” was coined. This would come from the Nahuatl language and is formed by the roots; Ne – personal -; pohual or pohualli – the account -; and tzintzin – small similar elements. This could be considered to translates into: counting with small similar elements by somebody.
On the other hand in a 1746 book Lorenzo Boturini (ref 14a) mentions : “Similarly, there arose in this age a new way of preserving history, and it was with long cords, in which were interwoven other thin ones that hung from the principal cord with knots of different colors. In the kingdoms of Peru these cable histories [Historias Funiculares] were called quipu, and in those of New Spain nepohualtzitzin, deriving their names from the adverb nepohualli, which means eighty, or as if we would say, cord of counting and number, in which are recorded and enumerated things worth remembering, both divine and human. (p. 135)”. In Rémi Siméon’s 1885 Nahuatl-Spanish dictionary (ref 14b), the Nepohualtzintzin refers to “Threads of different colors that, knotted in different ways, served, like the quipus of Peru, to remember memorable events; but this custom seems not to have been continued by the ancient Mexicans except in very remote times.”
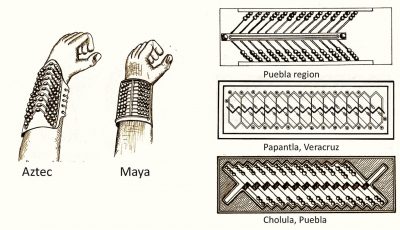
There is no trace of any surviving mexican abacus type device with beads. The ideas about such an abacus come entirely from reconstructions of the Mexican David Esparza Hidalgo, based on some old engravings (ref.15a; see images below) and his undocumented oral interviews. Esparza called his device Esparza’s calculator. There is also a report by Domingo Yojcom Rocché from Guatemala, that he identified a similar gauntlet type Mayan Abacus he called Jik’ob’al (ref.15b) on archological sites in Guatemala like the La Amelia and Cancuén in the Peten region. The image here shows a Cancuén panel portraying the ruler Tajal Chan Ahk, whose forearms show bead covered gauntlets. But were these decorative or meant for calculations? Esparza also refers to a Bonampac mural in Chiapas, where ona can see at the bottom figures kneeling and handling strings of beads, which might have been for counting.
Esparza’s Nepohualtzintzin abacus is based on a vigesimal, base 20 counting system. The abacus has 13 rows of seven beads corresponding to a total of 91, which was related to the number of days in a season. Four seasons coresponded to a year of 364 days (1-1/4 days short). The seven beads are arranged in a 4+3 configuration. The four beads correspond to units, whereas the three to multiples of five. The abacus possibly also existed as a wearable calculator: in the form of a gauntlet (see e.g. a video on this here) as shown in a still form that video. Whatever the historic reality of its origins, this abacus has found its way into teaching maths in schools.
The Lee Kai-Chen “improved” abacus. In the 1950s Lee Kai Chen invented an improved double deck abacus (image above). The lower deck is a 13 rod 5+2 Chinese abacus, whereas the upper deck is an 18 rod 4+1 bead one. The 5+2 lower deck incorporates a place setting vernier band, adjustable using a small wheel on the side of the frame. The Lee abacus was devised with the idea of optimising and speeding up multiplication and division with big numbers or calculations of square and cubic roots. Explanations on how to use this abacus may be found on the Lee Kai Chen Manual website.
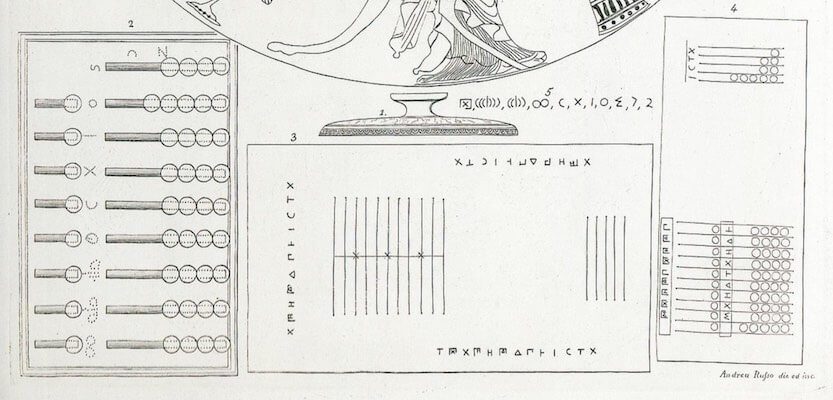
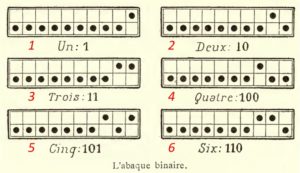
The “Universal” counting board and the Binary Abacus. In an 1893 book on Mathematical games, the French mathematician Edward Lucas (ref.16) suggested using a 10 x 10 chess board as a decimal counting board that he called the universal abacus. Beads or pins in each column could be used to count from 0 to 9 starting from the bottom. The board could be adapted to count in any base and in particular suggested to use it to demonstrate the binary system (see figures below).
In Lucas’ demonstration we have a one row with one bead per column system, but using several one bead rows ((several commercial abaci) ) as suggested by Robert Good (ref.17) would provide a nice illustration of addition, subtraction (by adding complements), multiplication, and division in a computer using several “registers”.
A Single String Abacus. Pace counting or ranger beads (see image above) are used to keep track of distance covered by counting the paces taken and are used in military land navigation. This podometer is usually made using a single set of 13 beads on a length of cord. The beads are divided into two sections, separated by a knot. There are nine beads in the lower section and four or more beads are used in the upper section. Typically when walking, one slides one lower bead on the cord for every ten paces taken. On the 100th pace, the nine beads in the lower section are pushed back away from the knot, and a bead from the upper section is slid upwards, away from the knot. In this manner, one can keep track of the number of paces taken or if the length of one pace is known the distance travelled.
Counting with Bead Garlands. It is a common practice in many religions (Christianity, Islam, Budhism,…) to count the number of recited prayers using a string of beads. In Islam, prayer beads are called Misbaha or Tasbih and have 99 normal-sized beads, (corresponding to the Names of God in Islam) and two smaller or mini beads separating every 33 beads. Buddhists use a Mala of usually 108 round beads, corresponding to mortal desires as decribed in Buddhist texts, with in some cases secondary pendant strings of recording beads (see below). One can also find bead counters for scoring in games like billiards.
The “Abacus in a Japanese Mala”. The heart of the Buddhist rosary is a large mother (head) bead and the main body of children beads, with counting going to or away from the mother bead. In some cases the mala is divided into two parts by a second large bead. In this case the first fifty-four beads represent, the fifty-four stages of the bodhisattva path. The mother bead has tassles attached to it via two short strings of smaller recorder or disciple beads (see a nice description in Tanabe 2012 (ref 18)). These are moved up the string, as in an abacus, every time a round of recitations is completed on the main strand. A second string of recorders is used to mark off the number of times the first string is exhausted, just like in a column of an abacus. At the end of the short strings there are teardrop shaped stoppers.
In some cases the secondary strings were eliminated but some Buddhist schools (Shingon, Tendai, Nichiren, and Jōdo ) maintained these. More recent versions of some rosaries (Shingon and Nichiren) have four and sometimes five strand of record beads. The Tendai ones tend to have two strands attached to the main mother bead, one strand having twenty small beads, the other with ten slightly larger ones. There also exists a curious intersecting ring mala dating from the 16th century, and used by the Jodo sect today, which has two intersecting rosaries : a 36 bead rosary with a second 30 bead rosary, allowing 1080 recitations. Two recorder strings with six and ten beads were attached via two metal rings to the second rosary. This allowed a total of 64800 recitations. Today the standard is 40 and 27 beads or sometimes 27 and 20.
Some further examples of various abaci may be found in the collection page here.
Some recent educational abaci of special types.
Unusual abaci. In these images you can see some unusual abaci and what look like counting devices of a unique type. They were probably made to specific order, while some seem to be of the “do it yourself ” type. Why were they made?
Some more artworks.


REFERENCES.
1.Marco Polo. The Travels of Marco Polo, Volume II(Translated by Sir Henry Yule & Henri Cordier in 1903) Dover Publications (1993)
2. Discover Hishango. Royal Belgian Institute of Natural Sciences, Brussels, Belgium
3. V. Pletser, D. Huylebrouck, ‘The Ishango Artefact: the Missing Base 12 Link’, Forma, 14- 4, 339-346, 1999
4.O. Keller, ‘Les fables d’Ishango, ou l’irrésistible tentation de la mathématique-fiction’, Bibnum, https://www.bibnum.education.fr/sites/default/files/Ishango-analyse.pdf, août 2010.
5.V. Pletser, D Huylebrouck , Contradictions and narrowness of views in” The fables of Ishango, or the irresistible temptation of mathematical fiction”, answers and updates (in English and in French … – arXiv preprint arXiv:1607.00860, 2016 – arxiv.org
6.Peter Rudman, How Mathematics Happened: The First 50,000 Years. Prometheus Books, Amherst, NY, 2007. ISBN 978-1-59102-477-4
7.Jonas Bogoshi, Kevin Naidoo and John Webb, “The Oldest Mathematical Artefact”, The Mathematical Gazette, vol. 71, no. 458, Dec. 1987.
8. Website of Denise Schmandt-Besserat, University of Texas: http://sites.utexas.edu/dsb/
9. The Oxford Handbook of the History of Mathematics, edited by Eleanor Robson, Jacqueline Stedall Oxford Universty Press, 2008, ISBN: 9780199213122
10. Marika Sardar, “Astronomy and Astrology in the Medieval Islamic World.” In Heilbrunn Timeline of Art History. New York: The Metropolitan Museum of Art, 2000–. http://www.metmuseum.org/toah/hd/astr/hd_astr.htm (August 2011)
11. Chris Weeks, “Counting Boards – A Counting Board in a Strasbourg Museum,” Convergence (June 2010)
12. George Watt. Indian Art at Delhi 1903. Being the Official Catalogue of the Exhibition 1902-1903. Motilal Banarsidas, Delhi 1903, 1987. ISBN : 81-208-0278_0
13. Raffaele Garrucci. Bulettino Archelogico Napoletano, N° 36, p. 93-96, December 1853. Heidelberg University Digital Archive. or https://archive.org/details/bullettinoarcheo01napo/page/88
14a. Boturini Benaduci, Lorenzo (2015) Idea of a New General History of North America, trans. Stafford Poole. Norman, OK: Univ of Oklahoma Press, 2015. [Idea de un nueva historia general de la América Septentrional, Madrid:Juan de Zuñiga, 1746].
14b. Rémi Siméon’s Nahuatl-Spanish, Diccionario de la lengua náhuatl o Mexicana (1885):
15 a. Hidalgo, David Esparza (1977). Nepohualtzintzin: Computador Prehispánico en Vigencia. (The Nepohualtzintzin: An Effective Pre-Hispanic Computer) (in Spanish). Tlacoquemécatl, Mexico: Editorial Diana.
15b. Yojcom Rocché Domingo 2015, Jik’ob’al – Ábaco Maya. Editorial Maya’ Wuj, Guatemala. ISBN 9929-634-24-X
16. Lucas Edouard, 1893. Récréations Mathématiques III. (p.53) Paris, Gauthier-Villaire et Fils.
17. Good Robert C. Jr., 1985. The Binary Abacus: A Useful Tool for Explaining Computer Operations. Journal of Computers in Mathematics and Science Teaching, 5, p34-37.
18. Tanabe George J., 2012. Telling Beads: The Forms and Functions of the Buddhist Rosary in Japan. Beiträge des Arbeitskreises Japanische Religionen. Universität Tübingen.
19. Kojima Takashi. 1954. The Japanese Abacus Its Use and Theory. Charles E. Tuttle Co. of Rutland, Vermont & Tokyo, Japan https://archive.org/details/japaneseabacus00taka