Simplifying Calculations: from the Multiplication Table to Napier’s bones and Logarithms.

Simplifying calculations: from the multiplication table to Napier’s bones and logarithms.

May, 2020. Vladimir Esaulov.

Today, most of us rarely do simple calculations by hand, but grab a pocket calculator (or a smartphone) and do all our additions subtractions and multiplications with it. We might still try to do this manually, but what about extracting a square root? Since the 70’s using an electronic calculator is so much easier, but children still need to learn the multiplication table: one of the first tables designed to help in calculations. Many years ago, in a world where few people studied, much effort was devoted to create simple devices that could aid in performing all kinds of tedious, yet essential, arithmetic calculation. In this page we have a quick look at these developments, starting with arithmetical/mutiplication tables and lattice multiplication and then at John Napier‘s famous logarithms and his calculation aids: the so called Napier bones, Multiplication Promptuary. At the end, some later variants of Napier’s rods are shown, including contributions of Wilhelm Schikard, Athanasius Kircher, Gaspard Schott, René Grillet, Samuel Morland, Pierre Petit, Jacob Leupold, Genaille-Lucas and a few others.

The First Multiplication Tables.

As some may remember, many old school notebooks, would systematically have a multiplication table on a cover page. So who invented the multiplication table? Many people. We look here briefly at some ancient tables. The interested reader can find a detailed description of ancient mathematics in e.g. the classical text of Neugebauer (1969).

Mesopotamia. Babylonian tables. Multiplication tables appear first on Babylonian tablets around 2000 BC. Small clay tablets were used to record documents and some were made for multiplication and calculating square and cube roots. An example is shown in the figure 1.

Babilonians used a characteristic wedge shaped cuneiform writing and had invented a sexagesimal, base 60, counting system, which we still use when speaking of angles or time in degrees, minutes and seconds. Their numbers went from 1 to 59, with no zero and had a place value system. For them division by n was a multiplication by a reciprocal, 1/n, number and so they made tables of reciprocals. Their multiplication tables had the peculiarity of going from 1 to 20 and after that they tabulated higher multiples of ten. So the final result was obtained by addition of the parts (e.g. 35xN= 30xN+5xN).

The Egyptian fractional tables. The main source of information regarding Egyptian mathematics comes from four surviving papyri (e.g. Imhausen 2016) and a few other objects (Akhmim wooden tablets, also known as the Cairo wooden tablets (Museum of Egyptian Antiquities, Cat. 25367 and 25368), a leather roll (British Museum BM10250, etc). These date to the time of the Middle Kingdom (2055-1650 BC ). The two main papyri, with large intact portions, are the so called Moscow or Golenishchev (Pushkin Museum of Fine Arts, Moscow E4676) and Rhind (British Museum, EA10058) papyri, dating from circa 1850 BC and 1550 BC. The other two, the Lahun (or Kahun; Petrie Museum of Egyptian Archeology, University College London.) and Berlin 6619 (Staatliche Museen Berlin) are very fragmented. The papyri generally list some problems pertaining to geometry with calculations of areas and volumes and include tables of divisions, multiplication and handling of fractions. The Egyptian way of calculating involved multiplication or division by two and additions, so that they did not require a full multiplication table of the type used now. These tables or parts thereof are found on the Rhind and Lahun papyrus and the leather scroll.

The close to 5 meter long, Rhind (Ahmes) Papyrus was discovered near Luxor, Egypt. Most of the papyrus is in the British Museum London and is named after Alexander Henry Rhind a British antiquarian. It was created by the scribe Ahmose (or Ahmes) who wrote down eighty-four problems including a 2/n table as well as a second smaller table of fractional expressions for the numbers 1 through 9 divided by 10. Ahmes notes that his scroll is a copy of older scrolls. It reports an odd n table up to 101. The Lahun papyrus IV.2 fragment reports a 2/n table for odd n, n = 1, , 21. The leather scroll contains sums of unit fractions.

The Greek table. The multiplication table as is commonly seen today is sometimes attributed to the Greek mathematician Pythagoras (570–495 BC) and in some countries is called the Table of Pythagoras.

The oldest surviving Greek multiplication table on a wax tablet (figure 3) is currently housed in the British Museum. It is dated to the 1st century AD, but could be from an earlier time (reference). A multiplication table was included in the work of Nicomachus of Gerasa (60–120 AD; Gerasa now Jerash, Jordan): Ἀριθμητικὴ εἰσαγωγή (Arithmētikē eisagōgē or Introduction to Arithmetic).

The Chinese multiplication table. A few years ago, a 2300 year old bunch of bamboo slips were discovered, possibly in the excavation of a tomb (Qiu 2014). These are now in the Tsinghua University Arts Museum. The bunch included 21 slips (Figure 4), giving one of the probably oldest known recording of the decimal multiplication table (Suanbiao). They correspond to the period of the Warring States (circa 305 BC).

The bamboo slips are 7 to 12 millimetres wide and up to half a metre long slips. The top row and the rightmost column contain, arranged from right to left and from top to bottom respectively: the number 0.5; the integers from 1 to 9; and multiples of 10 from 10 to 90 (Qiu 2014). The entries at the intersection of each row and column in the matrix provide the results of multiplying the corresponding numbers. The table can also help users to multiply any whole or half integer between 0.5 and 99.5. Numbers that are not directly represented, would have to be converted into a series of additions. The table could be used to do divisions and find square roots, although its actual uses are unknown.

Napier’s Logarithms, Rods and Promptuary.

John Napier of Merchiston (1550 –1617) was a Scottish mathematician (Seath 2017, Hobson 1914, Gibson), whose name today generally evokes the invention of logarithms. John Napier published his work of many years in his first book (Napier 1614) : Mirifici Logarithmorum Canonis Descriptio (A Description of the Wonderful Canon of Logarithms) in 1614. This book presented the idea of logarithms briefly, along with a set of tables of logarithms calculated by Napier and instructions of use with examples in trigonometry. A full description of their construction appeared later, in Canonis Construcio (Napier 1619). This, although probably written before the publication of the first one, was published posthumously by his son Robert Napier, with comments by mathematician professor Henry Briggs (1561-1631), with whom Napier interacted strongly, as mentioned later here.

Logarithms became immediately highly popular with academics and acclaimed enthusiastically by the astronomer Johannes Keppler. In his time, Napier, however, became famous outside academic circles, for the invention of two popular calculating aids: the Napier bones or rods and the Promptuary described in his 1617 book Rabdologiae (Napier 1617). The book also describes his chessboard abacus presented elsewhere here on ancient calculating instruments and the abacus. Napier here also, for the first time, described the use of the decimal point. The invention of decimal fractions is due to earlier work of Simon Stevin (1548-1620), published in 1585.

One of Napier’s aims for many years had been the attempt to simplify and speed up calculations, in an epoch, when for navigation of ships and astronomy accurate lengthy calculations had to be performed and creation of tables of trigonometric functions was the object of much labour.

In his words, in Mirifici Logarithmorum: “Since nothing is more tedious, fellow mathematicians, in the practice of the mathematical arts, than the great delays suffered in the tedium of lengthy multiplications and divisions, the finding of ratios, and in the extraction of square and cube roots– and in which not only is there the time delay to be considered, but also the annoyance of the many slippery errors that can arise: I had therefore been turning over in my mind, by what sure and expeditious art, I might be able to improve upon these said difficulties. In the end after much thought, finally I have found an amazing way of shortening the proceedings, and perhaps the manner in which the method arose will be set out elsewhere: truly, concerning all these matters, there could be nothing more useful than the method that I have found. For all the numbers associated with the multiplications, and divisions of numbers, and with the long arduous tasks of extracting square and cube roots are themselves rejected from the work, and in their place other numbers are substituted, which perform the tasks of these rejected by means of addition, subtraction, and division by two or three only. Since indeed the secret is best made common to all, as all good things are, then it is a pleasant task to set out the method for the public use of mathematicians. Thus, students of mathematics, accept and freely enjoy this work that has been produced by my benevolence.”

Logarithms, the Background and the People. Accurate navigation at sea, being the focus of many calculations, Napier’s work on logarithms discusses them for trigonometric functions. Logarithms, as many of you know today, allow replacing the unpleasant task of multiplying or dividing numbers by simple additions or subtractions. In Napier’s times there already existed several relevant ideas which could be seen as serving as the background for the development of logarithms. We saw above that the multiples of two were known from very ancient times. It was known that there is a direct relationship between arithmetic and geometric progressions: e.g. 0, 1,2,3,4,5,6,7, … and 1,2,4,8,16,32,64,128, 256… From a comparison of these series one can deduce that the sum of two terms in the arithmetic progression say 3+5=8 gives the position of the term in the geometric series (8th) that is the product of the corresponding terms (3rd and 5th)) in the arithmetic series, i.e. 8×32=256. In other words, as we now know, the powers of 2 are added (2³x2⁵=2⁸), although this was not common knowledge at the time. The German mathematician Michael Stifel (Stifelius) (1487-1567) presented for the first time the idea of an exponent in his Arithmetica integra 1544. He gave the correspondence between these arithmetic progression and geometric progression and also extended it to zero and negative powers, so that 0 corresponded to 1, -1 corresponds to 1/2, -2 corresponds to 1/4, etc. He did not, however, go beyond this. Another useful bit of knowledge in those days was, that the product of sines (cosines) could be expressed via a sum: 2sin(a)xsin(b)= cos(a+b) +cos(a-b), a solution method known as prosthaphaeresis.

Napier’s discussion of logarithms presented his definition of the logarithm in terms of movement of two points along infinite (bi) and finite (TS) lines with constant and decreasing velocities respectively as shown in his sketch from Canonis Constructio given in figure 5. The latter, variable velocity, was proportional to the remaining distance. One deals here with an arithmetic (fixed velocity) and a decreasing geometric progression. Napier defined numerically the distance bc travelled with constant velocity along bi (as the logarithm (or artificial number as he then called it) of the remaining distance (dS) to be travelled with the variable velocity. In presenting his tables he stressed the need for very large numbers in order to obtain high accuracy and in doing this he extended his initially chosen seven significant digits by seven extra ones beyond the “decimal point”, that he explicitly introduced for the first time in print (figure 5a).

A digression: the story of the decimal point is complicated and it is sometimes suggested that it was introduced by Bathrolomeus Pitiscus (1561–1613), the author of a famous text on Trigonometry (Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuus, 1595). Although Pitiscus knew decimal fractions, the introduction of this notation can not be attributed to him, as pointed out in the excellent text of Cajori ( see Cajori 1928 and Archibald 1949) about the history of the decimal point (and other mathematical notations). It is noteworthy that even today there is still hesitation between the use of a point and a comma…!

Note that the logarithms in Napier’s tables were not what are called today Napierian, or natural logarithms (denoted now by ln(x)), i.e. logarithms to the base e (e= 2.71828), but are closer to those to the base 1/e. In his tables zero corresponds to the logarithm of the 1000000 the large number chosen for the “full sine”. Logarithms to the base 10 came out of a collaboration with John Briggs, with the realisation by both, that a system of logarithms where log10= 1 (they discussed log 10= 10¹⁰) and log1=0 was much more practical. Briggs set out to compute logarithms for this system and eventually published a first short set of tables up to 1000 to 14 decimal places in 1617 (Logarithmorum chilias prima; “first thousand logarithms”). Later, in 1624, in Arithmetica logarithmica, he gave more extensive tables up to 20000 and from 90000 to 100000.

More complete tables were produced by others. In 1620, Professor Edmund Gunter (1581-1626) added calculations of eight figure tables of the logarithms of sines and the logarithms of tangents for each minute of the quadrant essential for accurate sea navigation and in astronomy. Keppler produced his own set of Napierian logarithms in 1624 with some additions and using a more rigorous approach. Adrian Vlacq a Dutch printer, published tables which completed those of Briggs, for numbers from 1 to 100000 with a 10 decimal place accuracy (Arithmetica logarithmica 1628) and included logarithms of sines and tangents. These served as a reference for a long time. The first logarithms to the base e, were published by John Speidell in his “New Logarithmes,” in London in 1619.

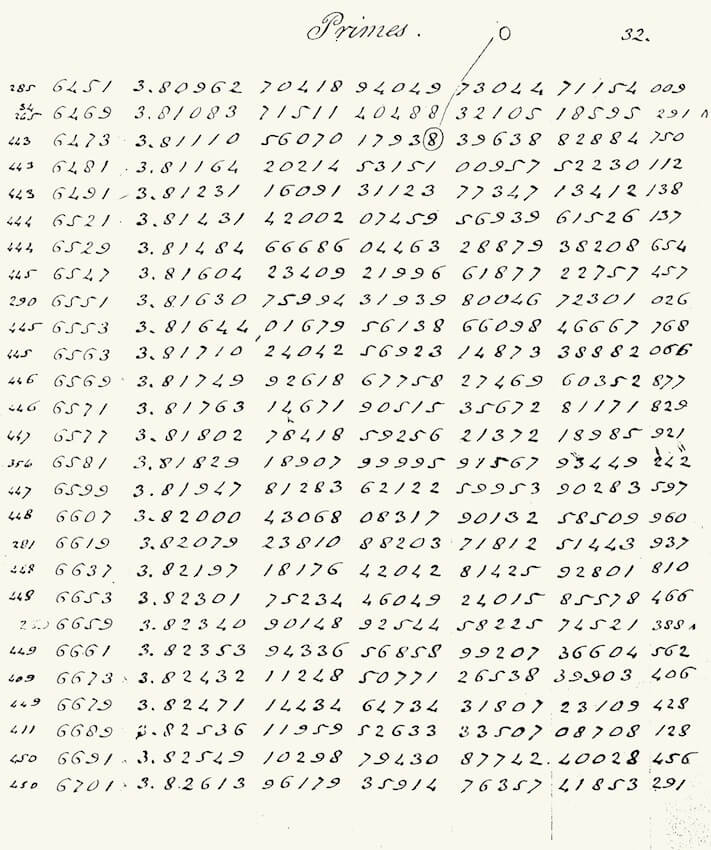
This description would be most incomplete, without mentioning the Swiss Jobst Bürgi (1552-1632), who had in the same years as Napier worked on his own version of what were in practice antilogarithms. These were only published much later in 1620 under the influence of Keppler. Finally one should mention the extensive effort at producing accurate tables by the human computer group of Gaspard de Prony in France (1794–1801), which were never published. One of the biggest, probably best, highly accurate, tables of logarithms was calculated in the late 19th century by the Scottish mathematician and engineer Edward Sang (1805 – 1890) and his two daughters, Jane Sang (1834 – 1878) and Flora Sang (1838 – 1925). Their 47 handwritten volumes (see Craik 2003), containing logarithms of numbers up to 370000, calculated manually to 16 places (some to 28 !! (figure 5c)), obtained much acclaim, but were never published for lack of funds.

Lattice Multiplication. Before describing Napier’s rods rods, we stop briefly on lattice multiplication. The provenance of this method of multiplication is unknown. It may have originated in India and from there travelled to Europe via, it is thought, China and the Islamic countries. It is mentioned in several 13^th-16^th century mathematics texts. In India this method is illustrated in the Gitamanjari (1545) of Ganesha and his comments on Bhaskara’s text on mathematics: Lilavathi (1150). Ganesha refers to it as the kapâta-sandhi method (see Datta and Singh 1935 and Hayashi 2013). It appears in the Islamic world first in the Moroccan text Talkhis amal al-hisab of Ibn al‐Bannāʾ al‐Marrākushī al-Azdi (1256–1321), and in Europe in texts by unknown authors: the latin text in England: Tractatus de Minutis Philosophicis et Vulgaribus (from around 1300) and in the Italian Larte de Labbacho (called also Treviso Arithmetic, 1478): the first arithmetic text published in the West. In appears in Luca Pacioli’s popular Suma de Arithmetica (Venice, 1494) and later is included in the Frenchman Oron Finé’s book on mathematics (Arithmetica practica, 1544), which was part of the French effort to revive mathematics teaching in France.

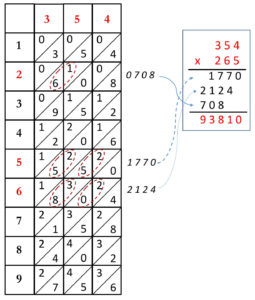
The method was called lattice multiplication, because the numbers to be multiplied are written on top and the side of a lattice of squares. Products of the numbers, corresponding to the column and row, are inscribed into these squares, as shown in the images here (figure 6), taken from the books of Pacioli and Finé. The layout of the lattice is reminiscent of the grids put up to protect windows in Venetian houses, and called gelosias (or graticolas) as mentioned by Pacioli and hence the method was called gelosia in Italian. In Arabic its name is aldarb alshabkiu (الضرب الشبكي) from lattice.

In the following we refer to the more common case of one of the numbers written on the right side. For the case of Finé’s example : 354×265, 345 is written above the squares and 265 on the right side of the lattice. The squares are divided by a diagonal line and each (two digit) product is inscribed into the resultant triangles as shown, with the tens digits above the diagonal. The result of the multiplication: 93810, is obtained by adding up the numbers along diagonals from the bottom right diagonal to the top left. When the sum results in more than one digit, then the value of the tens place is carried into the next diagonal.

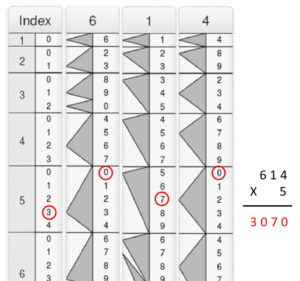
Napier’s Rods (Bones). In an effort to make multiplication, division and calculation of roots easy for the general public, even without the knowledge of the multiplication table, Napier proposed the use of a simple mechanical calculating tool: a set of square section rods, with which lattice multiplication could be easily performed. Why bones? Napier suggested the rods could be made of wood, silver or bone and one of the more elegant sets was made of ivory, whence possibly this name (figure 7).

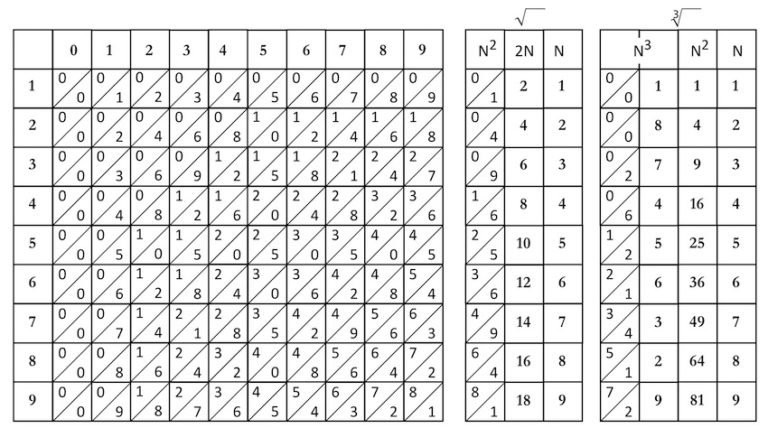
In order to simplify the work of doing multiplication, Napier suggested using a preconfigured set of ten, square section rods, for digits from 0 to 9 (figure 8a). The face of each rod is subdivided into ten squares, of the type you have in the lattice multiplication grid (figure 6). For a given number N, written in the topmost square, the face of a rod presents a column of numbers that are its multiples: from 1 to 9xN. These multiples are written with the digits split over the diagonal of the square. The rods are placed on a board with an extra rod marked with a reference column of numbers from 1 to 9. An ordered set of rods thus corresponds to the decimal multiplication table as shown in the figure. Multiple similar face rods were included to allow for presence of the same digits. With this set, large numbers could be multiplied without knowing the multiplication table just performing additions.

The use of the rods is illustrated on the example of the multiplication in Finé’s book: 354×265. The rods corresponding to 3, 5 and 4 are set side by side with the extra guiding rod. The rows corresponding to 2, 6 and 5 are used in the correct order of digits as shown. The sum of digits along diagonals in a row, as denoted here by ellipses, are written down. If necessary the tens place is carried to the next diagonal. The numbers from each of the three rows are added implementing an appropriate shift left to take into account for tens and hundreds. For divisions the bones serve as an aid for trial multiplications of the divisor, that one would have to do as usual to perform the operation. In figure 8a the two extra rods on the right are used to extract square and cube roots.

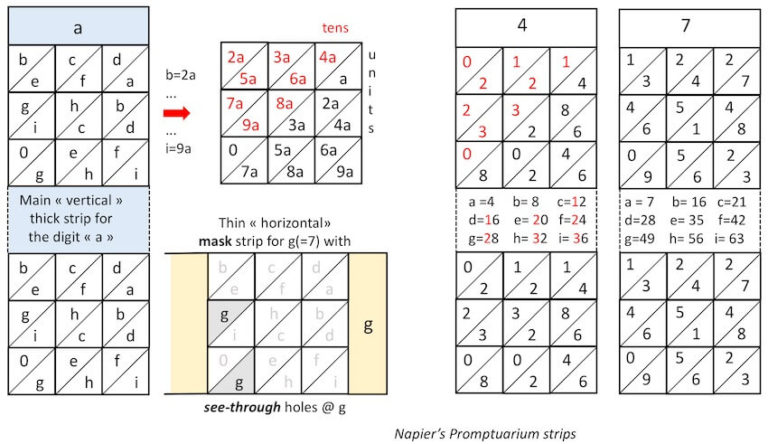
Napier’s Promptuary. Handling the multifaceted rods and tracking the numbers along diagonals, seemed cumbersome and to further facilitate and calculate more promptly, Napier came up with the idea of a Multiplication Promptuarium: a box (figure 9a) that stored a large number of slips (details in figure 9b, figure 10) with numbers somewhat similar to the rods and a second set of similar slips, with no numbers, but with specially cut triangular holes at specific positions.

The second type of slips, designed to be used by placing transverse to the first one, was used as a see-through mask to view numbers on the first set of slips. The rectangular slips were each marked with a digit from 0 to 9. The first type had nine large squares drawn on them, which were further subdivided into nine smaller squares bisected with a diagonal as shown in the figure10a. Napier designated each small triangle with the letters a, b,…i. On a slip designated by number N, the triangles were filled with numbers following the rule: a= N, b= 2N, c= 3N, … and i= 9N as shown in figure.. Napier left a blank place for zero, which is however indicated here for clarity. Here we illustrate the slips for numbers 4 and 7 as in Napier’s book. For two digit numbers, the tens digits were placed in the upper diagonal section (indicated here in red). The cut through triangles on the mask slip were in the positions corresponding to the slip number, as illustrated in figure for “g”, which corresponds to the multiplier 7.

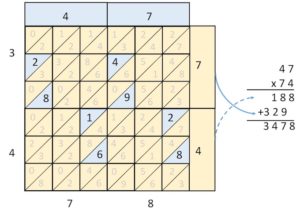
In order to multiply two numbers, say 47 x 74, two slips corresponding to 4 and 7, with numbered squares are placed (on top the Napier box) side by side to form the number 47 (blue slips) (figure 10b). The mask slips (yellow) corresponding to the number 74 are then overlayed transversely on top of the first two as shown (figure 10b). The product is obtained by adding all the numbers seen through the holes along the main diagonals, i.e. in this case 3478.

Napier’s Rods After Napier.

Several attempts were made to render the use of Napier’s rods more, in today’s words, user friendly. In some cases, especially in the later developments, they were complemented by tables of addition and even an adding device allowing to perform the intermediate additions. Thus in 1667 Sir Charles Cottrel proposed what he called an Arithmetical Compendium, which combined the rods with a sliding bead abacus. Versions of this system were made by the instrument maker Robert Jole around 1670 and can be seen in the Museum of Scotland (see image on this page) and Science Museum of Cambridge (inv; 34501).

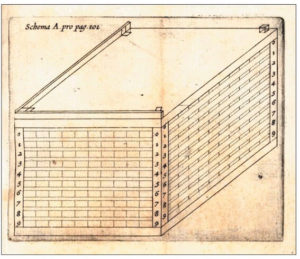
A number of these developments are described in e.g. the excellent paper of Williams (1983). Before briefly describing some of these here, we first note a beautiful box (figure 11) called “Organum Mathematicum”, integrating Napier’s rods along with a number of other similar “strips” covering various fields. It was designed in 1661 by Athanasius Kircher (1602-1680) as a mathematical teaching tool for the house of the Austrian Archduke Karl Joseph. The box, now in the Galileo Museum in Florence. The box was subdivided divided into nine compartments, for Arithmetic (Napier’s rods), Geometry, Art of Fortifications, Chronology, Horography, Astronomy, Astrology, Steganography, and Music. Each compartment contained 24 small strips with a colored triangular tip on which were inscribed definitions and information on the corresponding subject. One, black tipped, in each set constituted the application table, which provided instructions for the use of the set of strips. A description of it was given in the book of Gaspard Schott (1608-1666) along with many explanations supported by tables and illustrations and including his own ingineous variant of Napier’s rods.

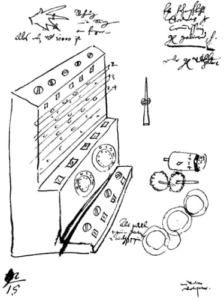
Schikard’s machine: the first ever four function calculator. In 1623 Wilhelm Schikard (1592-1635), had the ambitious aim to make a machine that combined a set of Napier’s bones and a mechanism to add the partial products they produced, so that the process of finding the product of two numbers was simplified. The machine, the Rechenuhr (Calculating clock), was constructed by him and described in letters to Johannes Kepler. Unfortunately it was then lost along with his notes. A copy built for Kepler, was destroyed in a fire. It was only recently built by Professor Freitag Löringhoff of Tübingen (Freitag Löringhoff 1978) , after some of Schikard’s letters and notes were found. Schikard’s sketch (figure 12) and a recent reconstruction is shown in the accompanying images here. A detailed description of the operation of this machine can be found in the article of Kisterman (2001). Basically the machine had two independent main parts: an upper part, which was a version of Napier’s rods for six digit number multiplication, with the particularity that instead of having the usual Napier rods, cylinders were used. Each cylinder had the full multiplication table inscribed on it for numbers from 0 to 9 and the appropriate part of the cylinder could be rotated to position it in front with the knobs located on top of the machine. A system of eight movable strips, for numbers from 2 to 9, (see image 12c) were mounted in front allowing to reveal only the numbers on the Napier “rod” strips, corresponding to the multiplication by a chosen number (see example on the German stamp shown here). The lower part of the machine, had the first ever toothed-wheel system designed to add and subtract, which also included a carry mechanism. It is thus the first known mechanical four-function calculator, although devisions would have to be carried out as usually with Napier’s bones. The last part of the machine was an aide mémoire, a “memory unit” , where intermediate results could be stored by positioning dials marked with numbers.

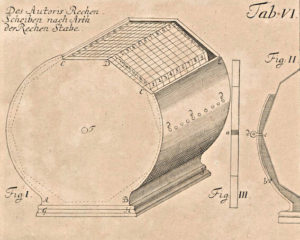
Other rotating cylinder/drum variants. Several other systems were later constructed with the general idea of putting the rods on rotating devices for easier consultation. Gaspard Schott in 1668, replaced the rods by a set of cylinders in a box (figure 13). All of Napier’s table from 0 to 9 was written on the surface of a cylinder so that it could then be rotated, with knobs on the front of the box, to expose the required digit on top. Two examples to be found at the National Science Museum London, dating from the end of the 17th century, are shown in the figure below.

A similar 19th century device incorporating a sliding bead abacus may be found in Vienna at the Technische Museum Wien (figure 14a). Another rotating cylinder machine, with Napier’s tables was built by René Grillet around 1678 (figure 15a). Its specificity was the inclusion of three sets of 8 dials on which were engraved numbers from 0 to 9 and their tens complements (see image later on this page). These were meant to record (upper two rows) and help in adding manually and temporarily “memorise” (third row) intermediate products from Napier’s tables.

Rotating drum versions (figure 14 b,c) were constructed by the Frenchman Pierre Petit (1594-1677) and the German Jakob Leupold (1674-1727). Petit described his Cylindre Arithmetique in his 1671 book. He made long bands of paper, on which were written sucessively the contents of the ten Napier rods. A number of such bands were mounted side by side on a wooden cylinder whose length depended on the number of digits one wished to have in calculations with large numbers. Pins, stuck on the bands, helped to advance them to bring forth the digits required in the calculation.

A somewhat different solution was adopted by Leupold, who designed ten sided, decagon disks. Each facet was inscribed with a set of Napier’s meltiplication grids for a given number. Several disks were mounted side by side and could be independently rotated and fixed in the desired position with a pin as shown here on Leupold’s illustration. The device is described along with many others in Leupold’s fascinating, 1727, illustrated book:”Theatrum Arithmetico-Geometricum“. A replica of this device may be seen in the Arithmeum museum in Bonn (Germany).

Morland’s rotating disk machine. In 1666, Samuel Morland (1625-1695), the inventor of several adding machines created a multiplying machine based on a set of circular disks on each of which were engraved the product numbers from the Napier bones in appropriate positions along the circumference (figure 15 b,c). The positioning was such that the two digits of a product were found at the opposite ends of a diagonal of a disk. The two large digits at the centre of each disk (figure 15c) indicated to which bones the double sided disk corresponded (upper digit face side).

The disks corresponding to the number to be multiplied were placed side by side on pinions in a straight line in the lower portion of the machine: e.g. 1734 in the figure 5b, in Morand’s example (there is an error in the engraving). They were covered by a hinged plate with small see-through product windows through which two digits, one from each adjacent disk could be seen. A rack and pinion device was used to rotate the disks using a key (GH in figure 15b) which also positioned a pointer (EF) on numbers from 1 to 9 which indicated the number by which the multiplication was done. The pairs of numbers appearing in the product window had to be summed. This operation was carried out for each digit of the multiplier and the results written down, to be added manually or using the Morland adding machine part (which did not incorporate a carry mechanism). Copies of the instruments may be found in the Istituto e Museo di Storia della Scienza (Museo Galilei), inv. no. 679 in Italy (shown here) and the Science Museum UK.

Concentric disk system. In 1728 J.M.Poetius described a sort of turntable system, in which the Napier rod tables were inscribed on the surface of ten concentric independently moving rings (Poetius 1728). Each ring had the full 1 to 9 set of the Napier table. Rings for the required digits could thus be brought side by side. Similar systems were proposed later by some others.

Genaille Lucas Rods. In 1891, Napier’s rods got a new revision. Two Frenchmen: the mathematician Edouard Lucas (1842–1891) and engineer Henri Genaille (18??–1903) proposed a new design that simplified operations, by eliminating the need to carry digits from one column to the next when adding intermediate products. Genaille designed a set of rods in which instead of the squares, one has nine rectangular sections with series of digits written vertically, with wide arrows (figure 16a,b) pointing from right to left (to a particular digit on the next rod to the left). An index rod set at the extreme left is used for the multiplier numbers. It has nine rectangles, for all the digits from 1 to 9.

To find the product of say 614 x 5, the index ruler and the ones for 6, 1 and 4 are set side by side (figure 16c). One chooses the fifth row, corresponding to the multiplier 5, using the index ruler. Starting with the fifth row of the rightmost ruler one then selects the topmost digit of this rectangular section, i.e. 0 in this case. One then just follows the arrows toward the left, and as may be seen one reads 3070. A version of these rods was also made using rotating cylinders as for the original Napier rods.

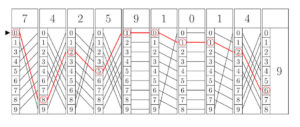
For the case of division, Genaille replaced the strips with the big shaded triangles by a special set with a multitude of single lines (figure 17 a,b). In this case one proceeds similarly to multiplication, but one goes from left to right from the index rod, from the divisor digit and follows the line arrows (figure 17c). The difference in this case is that one requires an extra remainder ruler (marked r here ) on the right-hand side to determine the remainder of the division operation, should this be necessary. Thus in the example of the division of 742591014 by 9 shown in figure 17c the remainder can be seen to be 6.

The Genaille Lucas rods became very popular and were used till around the1920s.

Napier rods in other bases. Napier and Genaille-Lucas rods have been made in bases other than 10 (see e.g. Roegel 2015, where you can also find instructions for use). Here we show hexadecimal rods. A higher resolution image for hexadecimal division rods, can be obtained here: SVG file.

References.

Andrews Frances E., 1928, The Romance of Logarithms, Journal of Applied Social Psychology, Volume28, Issue2, Pages 121-130. https://doi.org/10.1111/j.1949-8594.1928.tb05312.x
Archibald R.C. Bartholomäus Pitiscus (1561–1613). Math. Comp. 3 (1949), 390-397
Datta B. and Singh A.N. (1935) History of Hindu Mathematics. A Source book. Parts 1 & 2. Asia Publishing House. 1935 https://archive.org/details/HinduMathematics
Bürgi Jost, 1620. Arithmetische und Geometrische Progreß Tabulen/ sambt gründlichem unterricht/ wie solche nu ̈tzlich in allerley Rechnungen zugebrauchen/ und verstanden werden sol. Gedruckt/ In der Alten Stadt Prag/ bey Paul Sessen/ der Löblichen Universität Buchdruckern/Im Jahr/ 1620.
Cajori, F. 1928. “Did Pitiscus use the decimal point?” (p. 317-323) in his book: A History of Mathematical Notations ), v. 1, The Open Court Publishers. London Chicago, 1928.
Craik Alex D.D.2003. The logarithmic tables of Edward Sang and his daughters, Historia Mathematica 30(1), 47–84.https://doi.org/10.1016/S0315-0860(02)00018-6
Freytag-Löringhoff, Bruno Baron Von. 1978. “Die Rechenmaschine.” In Wilhelm Schickard, edited by Friedrich Seck, 288–309. Tübingen: J. C. B. Mohr (Paul Siebrck).
Gibson, George A. Napier and the Invention of Logarithms. in “Modern Instruments and methods of Calculation. A handbook of the Napier Tercentecary Exhibition”. ed Ellice.M.Horsburgh. London: G.Bell & Sons. and the Royal Society of Edinburgh
Grillet René, 1678. Nouvelle Machine d’Arithmetique. Journal des Scavans p 170. (see Theatrum Arithmeticum of Jakob Leupold (1727), page 26)
Hayashi Takao. 2013. Ganitamanjari of Ganesha, Indian Journal of the History of Science, 48(3)
Hobson E.W. 1914, John Napier and the invention of logarithms, 1614. A lecture by E.W.Hobson, Cambridge: at the University Press, 1914.
Imhausen Annette. 2016, Mathematics in Ancient Egypt: A Contextual History. Princeton Universty Press, ISBN 978-0-691-11713-3
Kistermann, F. 2001. How to use the Schickard calculator. IEEE Annals of the History of Computing, 23(1), 80–85. doi:10.1109/85.929917
Leupold, Jakob 1727. Theatrum Arithmetico-Geometricum, das ist: Schau-Platz der Rechen- und Mess-Kunst – darinnen enthalten dieser beyden Wissenschafften nöthige Grund-Regeln und Handgriffe so wohl, als auch die unterschiedene Instrumente und Machinen … : den annoch beygefüget: Die Theilung aller Linien, insonderheit …Gleditsch. Zunkel.Leipzig, 1727 (ETH-Bibliothek Zürich, Shelf Mark: Rar 10397. http://dx.doi.org/10.3931/e-rara-28852
Morland, Samuel. 1673. :The description and use of two Arithmetick Instruments : together with a short treatise, explaining and demonstrating the ordinary operations of Arithmetick. As likewise, a perpetual almanack, and several useful […]. London : printed, and are to be Sold by Moses Pitt, 1673. ETH-Bibliothek Zürich, Rar 51, https://doi.org/10.3931/e-rara-56520
Napier, John. 1617. Rabdologiae seu numerationis per virgulas libri duo: Cum appendice de expeditissimo multiplicationis promptuario. Quibus accessit & arithmeticae localis liber unus.
“Rabdologiae, or the calculation with rods in two books. With an appendix on a useful device for multiplication. And one book on local arithmetic. Edinburgh. Pub.Andrew. From Tomash Library on the History of Computing with English comments. Hart, 1617. https://ia801607.us.archive.org/2/items/rabdologiae00napi/rabdologiae00napi.pdf
Napier, John. 1614. Mirifici Logarithmorum Canonis Descriptio, Eusque usus, in utraque Trigonometria, ut etiam in omni Logistica Mathematica, Authore ac In-ventore, IOANNE NEPERO, Barone Merchistonii, Edinburgi 1614. https://archive.org/details/logarithmorumnapi/mode/2up
Napier John, 1619. Mirifici Logarithmorum Canonis Constructio; et eorum ad naturales ipsorum numeros habitudines; una cum appendice, de aliâ eâque præstantiore logarithmorum specie contenda. Quibus accessere propositiones ad triangla sphærica faciliore calculo resolvenda: Unà cum annotationibus aliquoot doctissimi D. Henrici Briggii, in eas & memoratam appendicem. Edinburgh. Pub; Andrew Hart
Neugebauer Otto. 1969. The Exact Sciences in Antiquity. Published Dover Publications (first published June 1st 1957)
Oronce Finé (Orontii Finaei) 1544. Arithmetica practica, in compendium per authorem ipsum redacta, multisque accessionibus locupletata … Paris, Apud Simoneum Colinaeum (https://archive.org/details/bub_gb_WkGIGZ-kCqsC/mode/2up)
Williams Michael R. 1983. From Napier To Lucas: The Use Of Napier’s Bones In Calculating Instruments. Annals of the History of Computing 5 , N° 3, pp.279 – 296. DOI:10.1109/MAHC.1983.10080
Pacioli Luca, 1494. Suma de arithmetica geometria proportioni (et) proportionalita. Venice : Paganinus de Paganinis (https://archive.org/details/summadearithmeti00paci/page/n3/mode/2up)
Petit, Pierre. 1671. Dissertations academiques sur la nature du froid et du chaud: avec un discours sur la construction & l’usage d’un cylindre arithmetique, inventé par le mesme autheur. Paris : chez Olivier de Varennes, M.DC.LXXI. [1671]. From ETH-Bibliothek Zürich- https://www.e-rara.ch/zut/content/structure/20652554
Poetius,J.M.1728. Gründliche Anleitung zu der unter den Gelehrten jetzt üblichen Arithmetischen Wissenschafft. Frankfurt u. Leipzig 1728. https://reader.digitale-sammlungen.de/de/fs1/object/display/bsb10082579_00005.html
Qiu Jane, Ancient times table hidden in Chinese bamboo strips, Nature ( News and Comments, January, 2014). doi:10.1038/nature.2014.14482
Roegel Denis. 2015. Napier’s bones and Genaille-Lucas’s rods. [Research Report] LORIA – Université de Lorraine. 2015. hal-01198447
Schott Kaspar, . Organum mathematicum libris IX : reverendissimo ac celsissimo principi ac domino, D. Joanni Casparo…, administratori, ac ejusdem per Germaniam & Italiam, partesque transmarinas magno magistro, domino in Freudenthal, Ellenberg, &c. : opus posthumum / explicatum à P. Gaspare Schotto e Societate Jesu, quo per paucas ac facillime parabiles tabellas, intra cistulam ad modum organi pneumatici constructam reconditas, pleraeque mathematicae disciplinae, modo novo ac facili traduntur. https://www.e-rara.ch/zut/content/titleinfo/6651236
Seath Garry, 2017. Beyond Logarithms and Bones. A Short History of John Napier and his Legacy. https://www.napier.ac.uk/~/media/images/special-collections/john-napier-400-book–electronic-format.pdf (A Napier’s 400^th centenary publication).
Weiss Stephan (2007). Die Rechenstäbe von Neper, ihre Varianten und Nachfolger.
(Napier’s rods, their variants and successors;
in German) From the website of Stephan Weiss: http://www.mechrech.info/publikat/Neper85Au.pdf